Space-Filling Polyhedra

Or finding shapes that tesselate in 3D

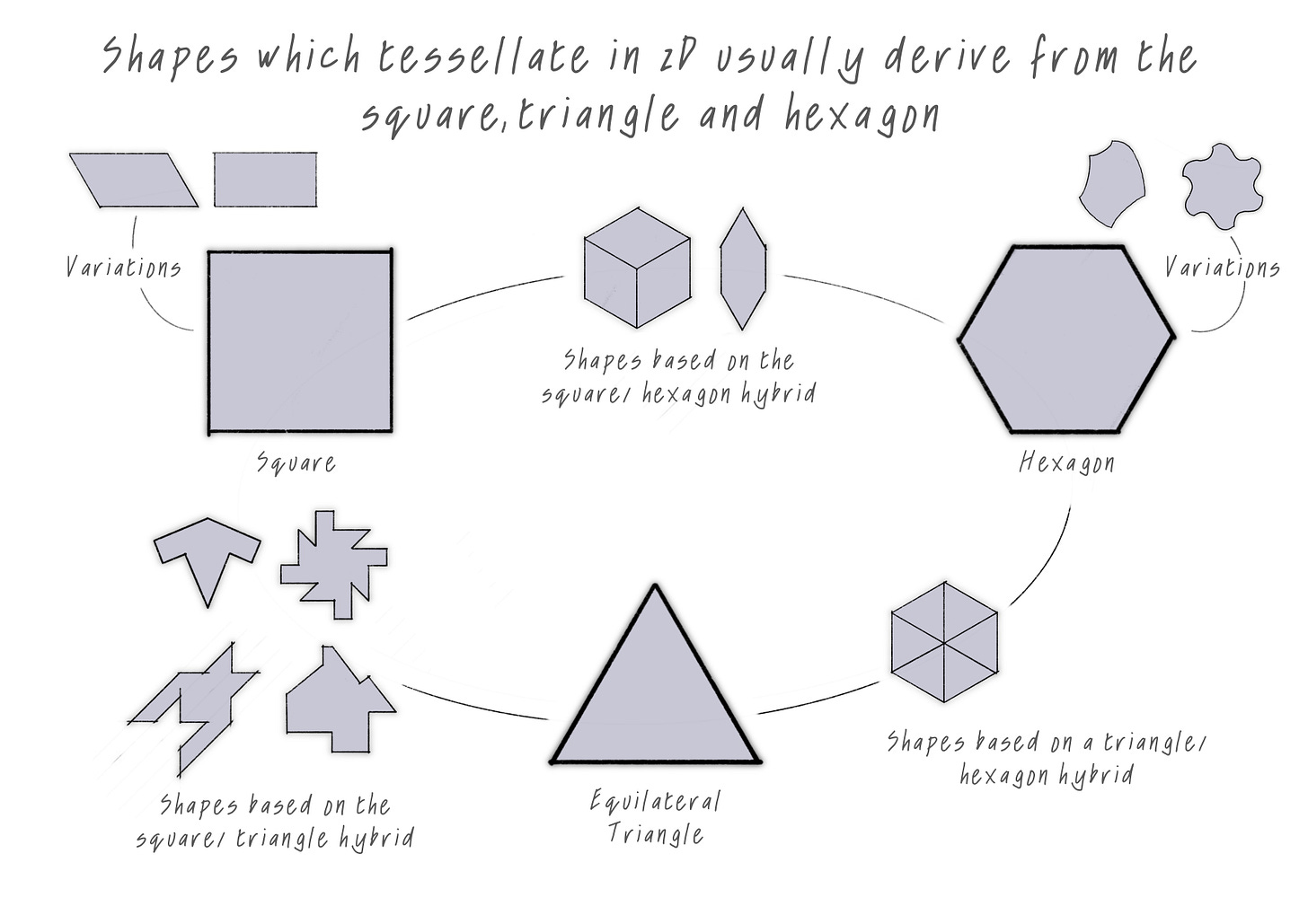
You know how some shapes tesselate in 2D? These are single shapes that fit together without leaving gaps, when arranged on a flat surface. Squares, triangles and hexagons are the main ones. You will have seen how this works with floor tiling and honeycombs in bee hives.

But if you have ever wondered which shapes tesselate in 3D, read on. There are some surprising examples which you would not believe actually fit together without leaving gaps!

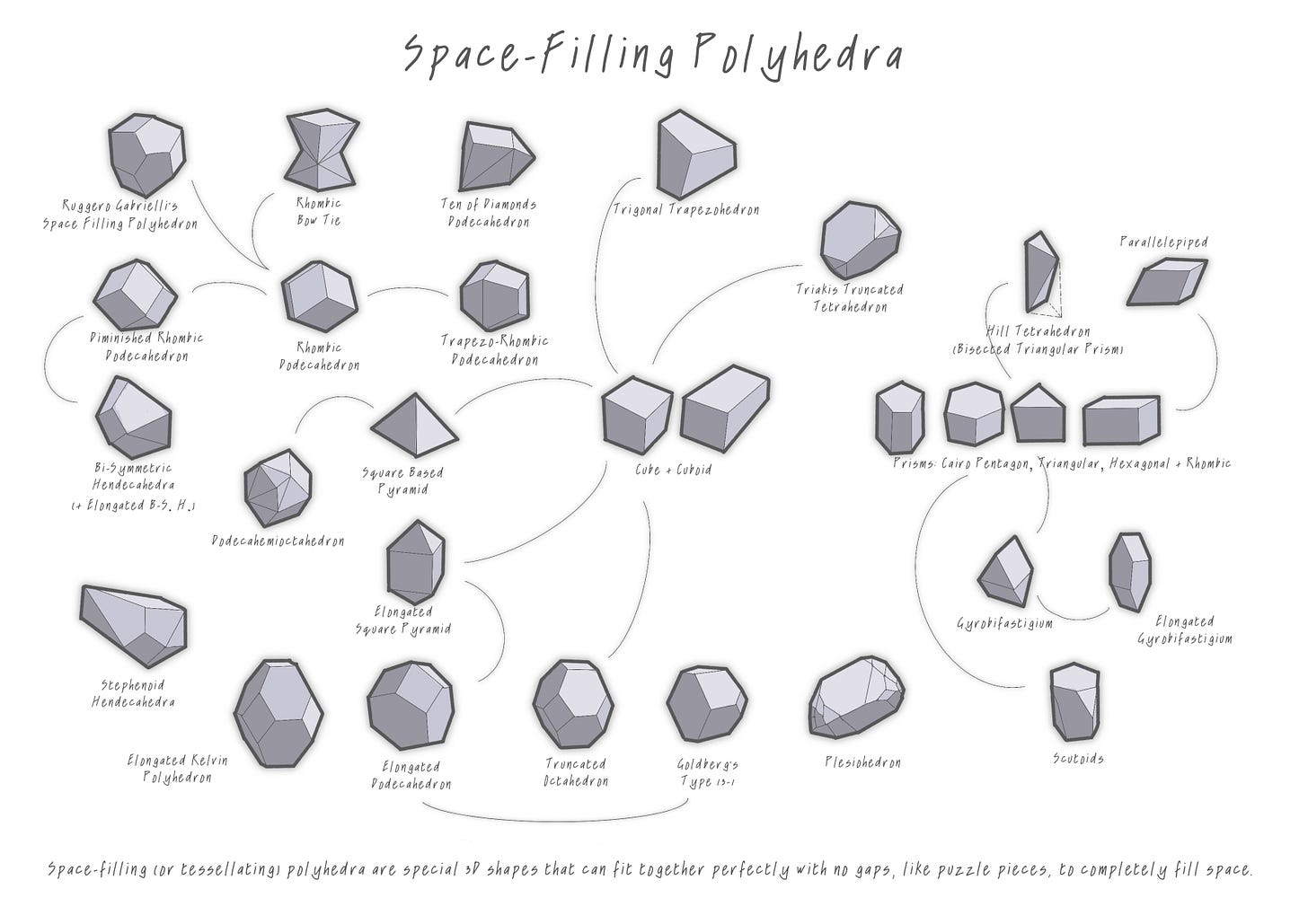
Imagine a world where shapes fit together perfectly like puzzle pieces in 3D space! Welcome to the exciting study of space-filling polyhedra. It’s a fascinating area of geometry where science, engineering, and architecture come together with some fascinating results.

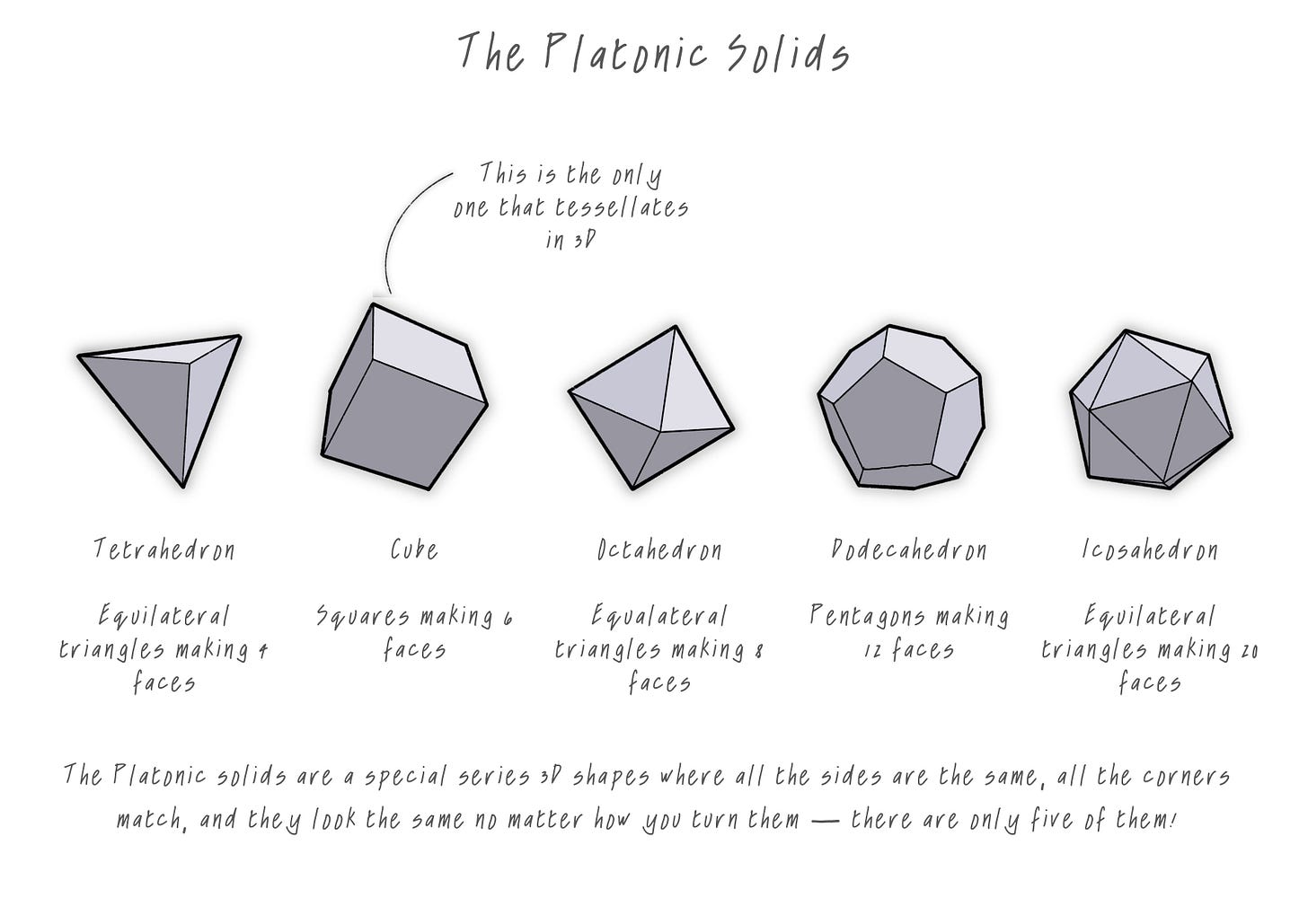
Did you know that the humble cube is the only Platonic solid that can tessellate in 3D? It's the classic building block of space-filling shapes, and the simplest, as you’ll see here…

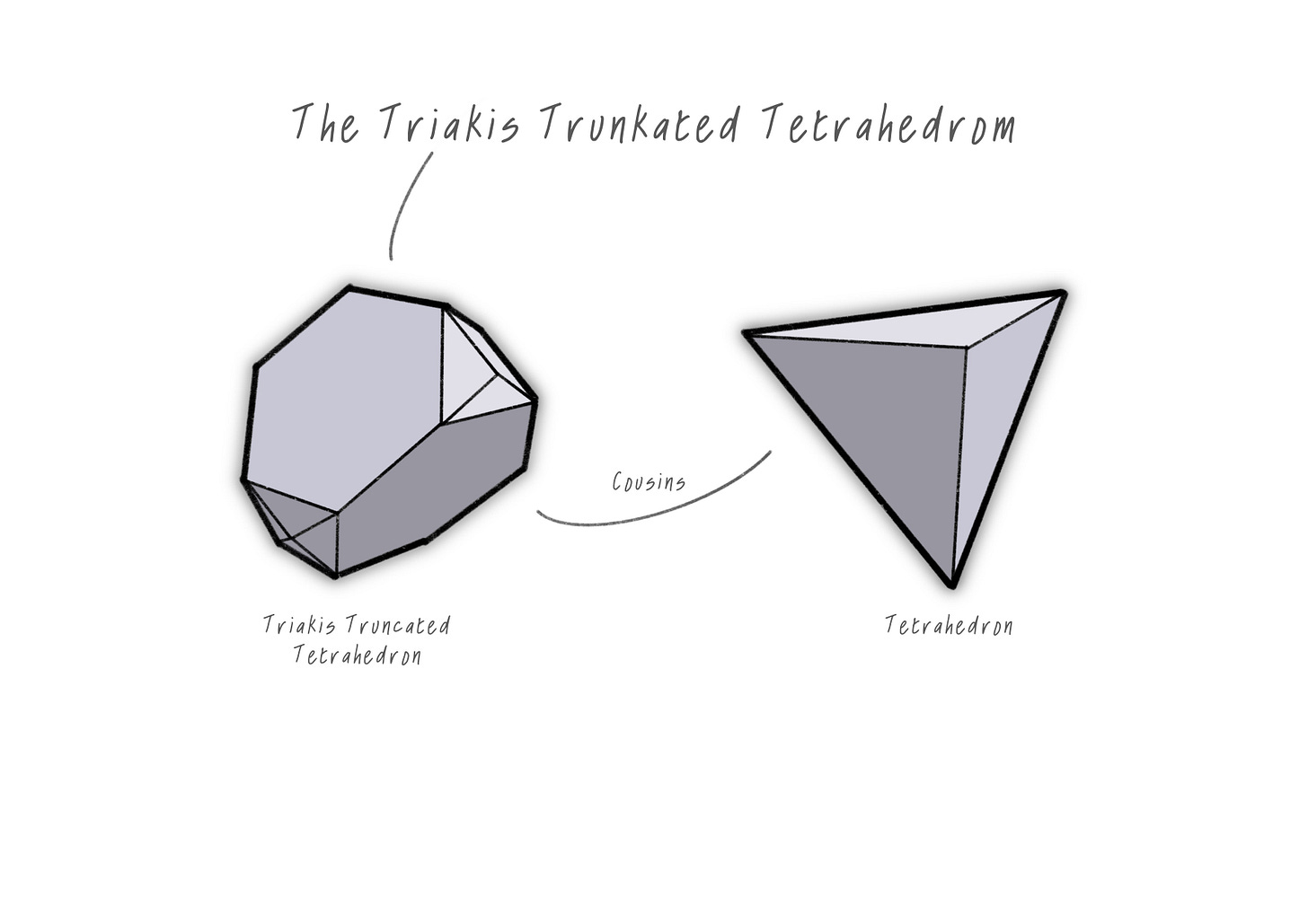
From here, there are tons of other fascinating forms to explore. For example, the triakis truncated tetrahedron is the closest 3D counterpart to the tetrahedron but has the super-power of fitting together seamlessly.

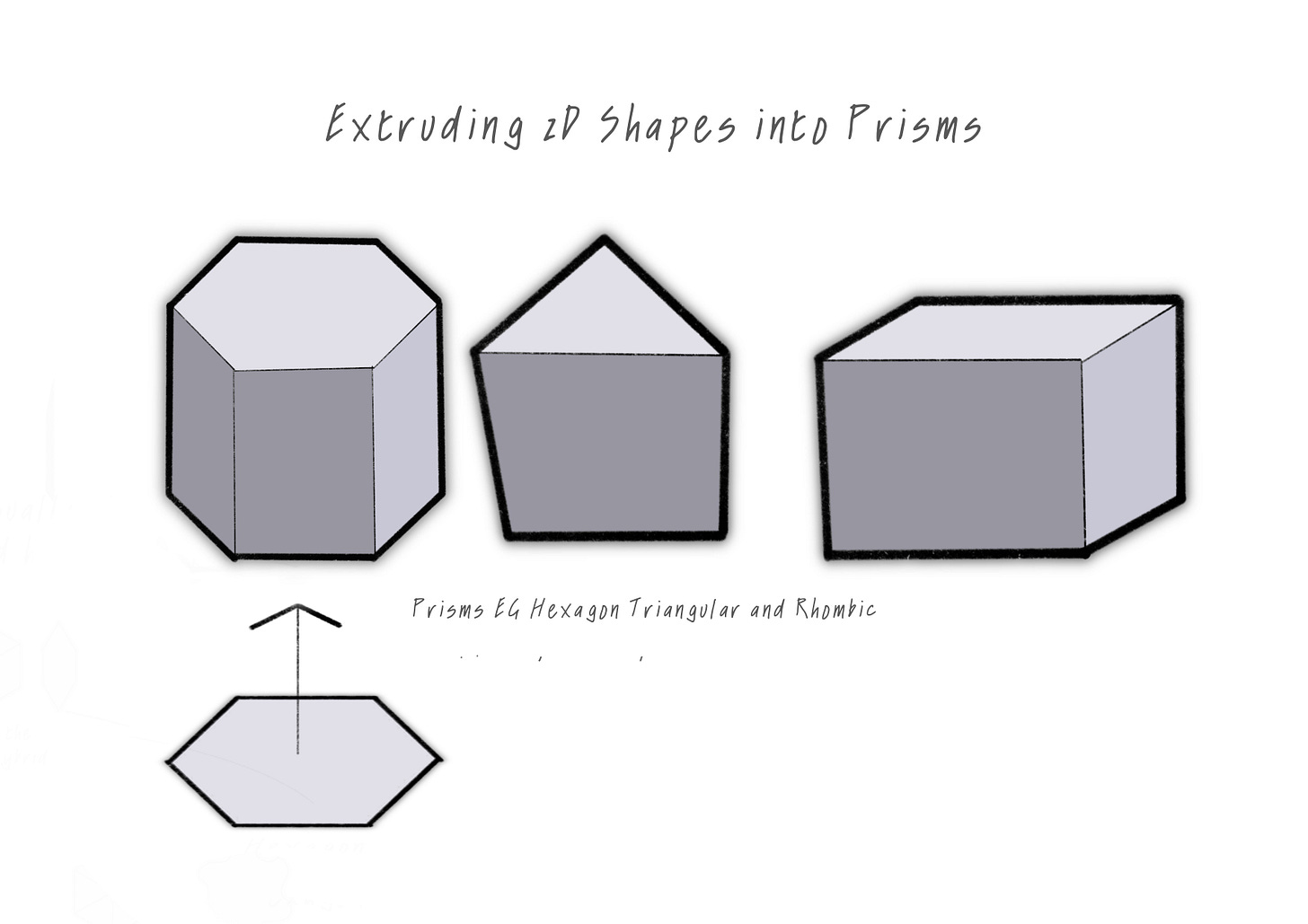
Here’s some easy wins: Shapes that tessellate perfectly in 2D, like squares and hexagons (as shown in the diagram above), can be extruded into ‘prisms’ to tessellate in 3D!

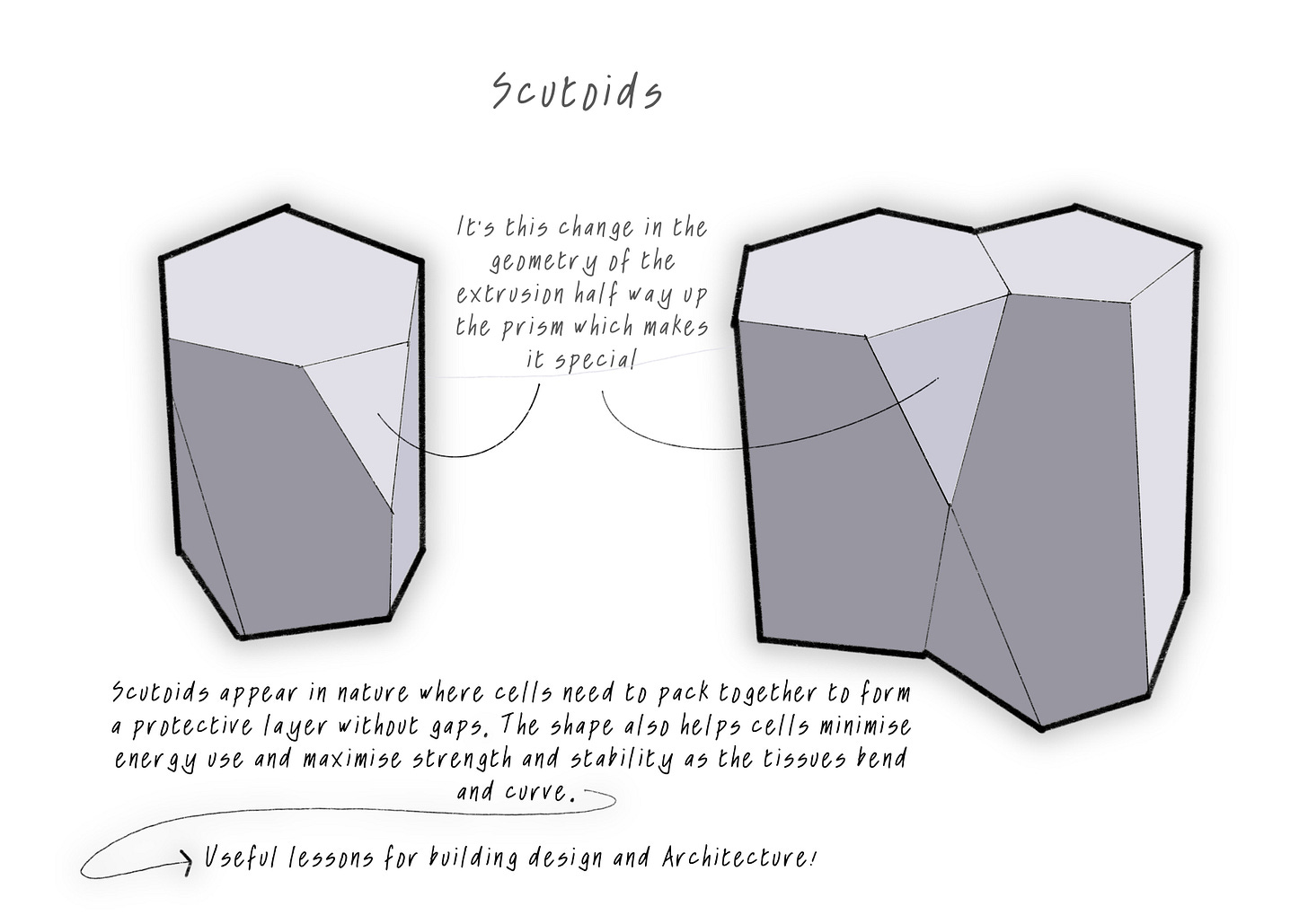
But we can do more with them to make them more interesting—When we slice, skew, or chop up these prisms, we get even wilder forms, like the scutoid—a shape that can be seen in nature, like in some cells that make up our vital organs!

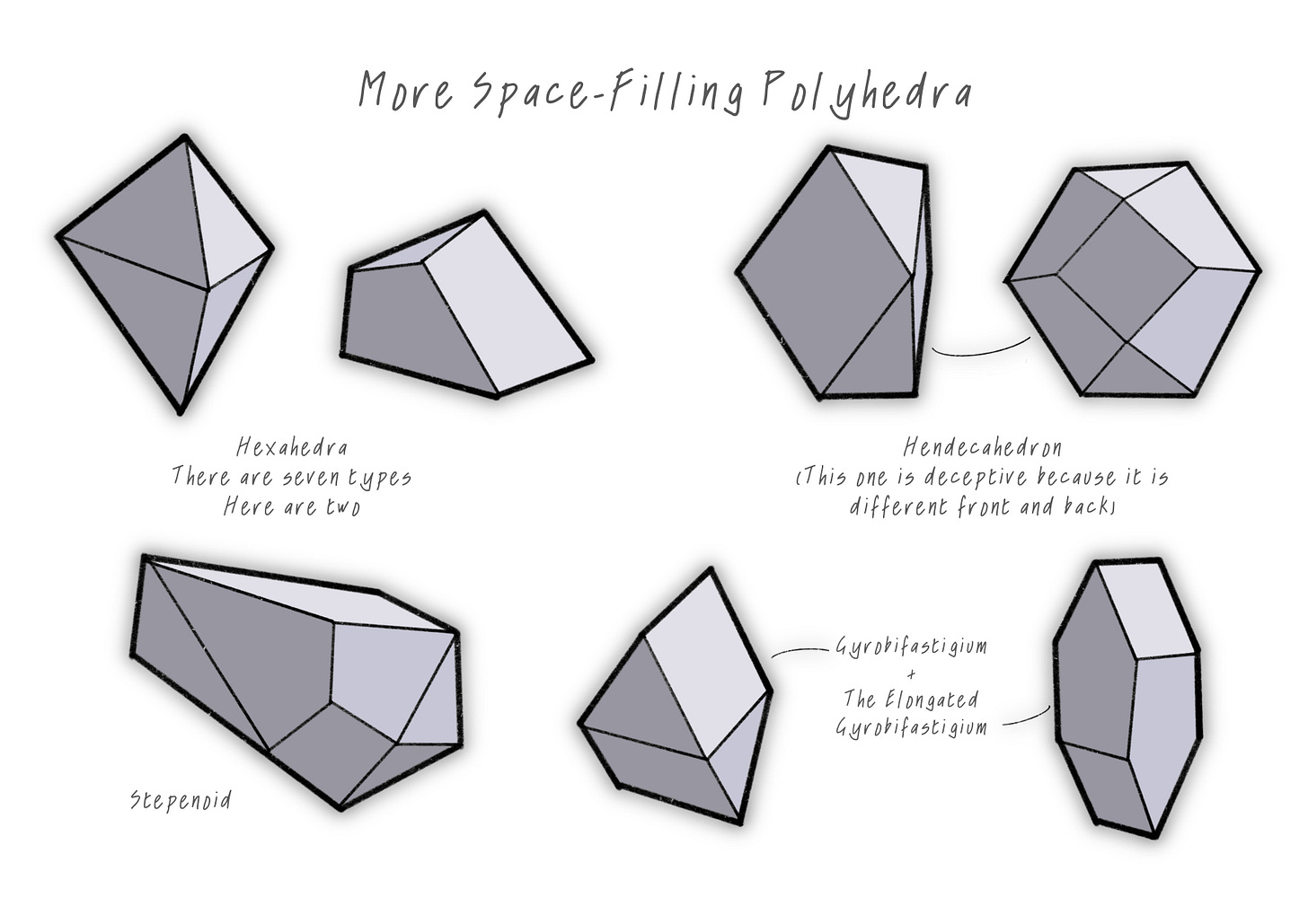
Dropping into even more complex geometry, there’s the gyrobifastigium, the hendecahedra, and the hexahedra—they're part of their own special families of shapes. Then there’s the square-based pyramid, a true multi-tasker—It acts as a bridge between shapes like the cube, the rhombic dodecahedron, and other more intricate forms like the elongated square pyramid.

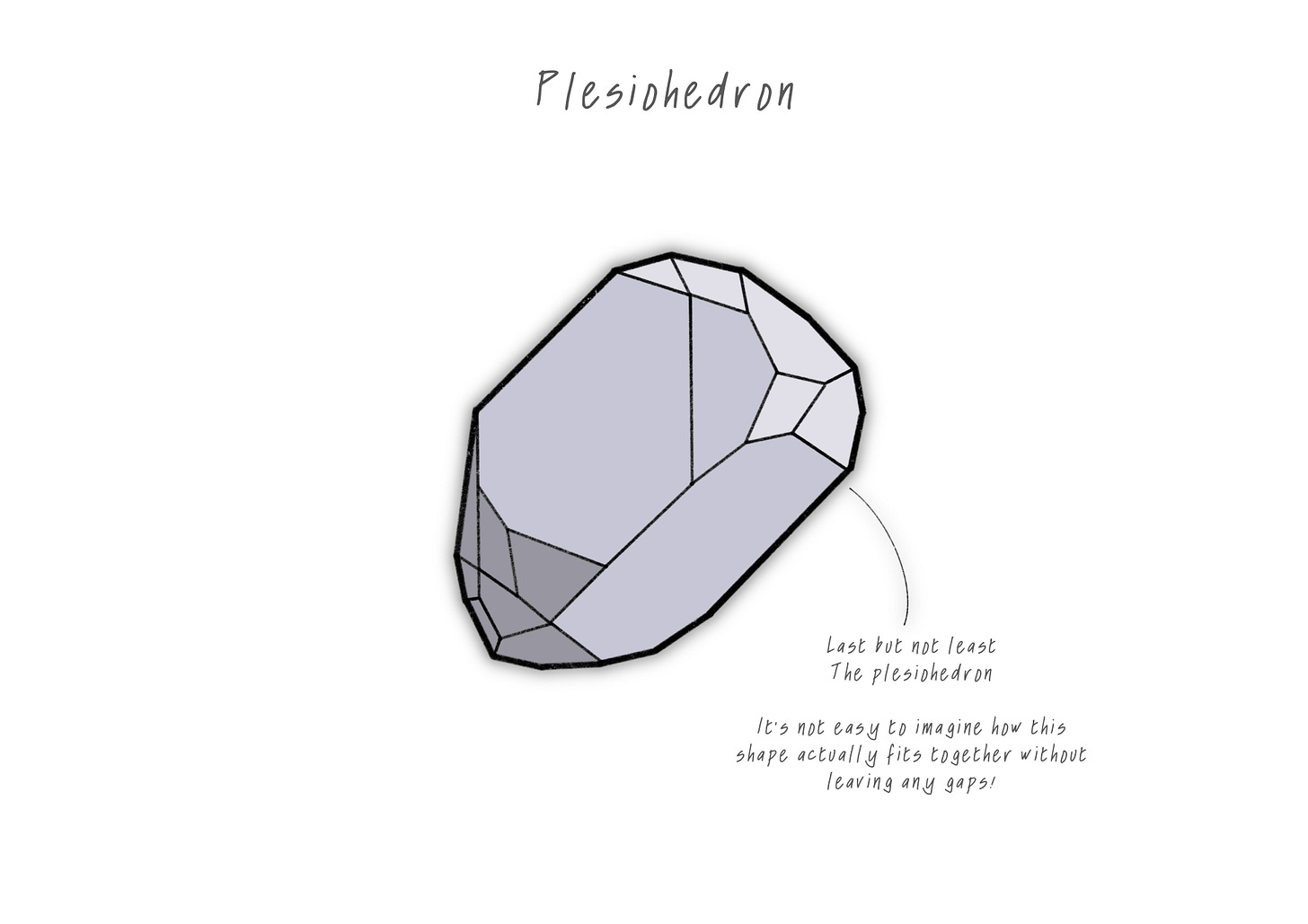
But wait—there’s more! Dive deeper into the world of complex geometries like the plesiohedron and the stephenoid hendecahedra—these shapes combine in dynamic ways to create entire collections of interlocking forms.

Why does this matter? For architecture and design, understanding these space-filling polyhedra can (and will one day) lead to revolutionary, cost-efficient, and awe-inspiring structures! Just imagine using these shapes to build innovative skyscrapers, earthquake-proof houses and more structurally efficient bridges. Or entire cities with compact and intricate spaces which are highly efficient at housing lots of people, yet feel open and uncrowded. And they will be useful for energy efficiency—Space-filling polyhedra with a low ‘surface area to volume ratio’ will help to manage heat loss. And then there’s packaging—You’ve seen tins of beans on the shelves in the supermarket and recognised the spaces between the cylindrical cans? All that empty space is shipped with the product. Redesigning the packing using space-filling polyhedra would eliminate all that space and save logistical costs. There’s tons of possibilities.

So, if you love experimenting with LEGO, or are intrigued at how honeycombs are so efficient, you’re already thinking like a space-filling polyhedra expert. This is geometry on a mission, and it’s a playground for innovation and imagination with possibilities yet to be discovered!

We hope you enjoyed this post. If you did, please share it on the button below. We love experimenting with geometry to see what it can offer Architecture, Design and workshop fun and you can find out more about what we do on our website.

Thanks!